vs.

After browsing my first tutorial for sPatch Mike Clifton emailed me wondering if I really needed that many patches to model my bottle of coke. He pointed at me that people still tend to think in term of polygons, even when there are using Bezier patches therefore loosing part of their interest and wasting render time too. Well I must admit I wasn't too concerned with modeling efficiency and render time when I created my first tutorial, it just came as a will to share my experience ... but I must admit he was right. Rendering a scene with two of my coke bottles nicely covered with a Glass texture put my P133 with 32Mb on its knees. For the first time on this machine I experienced heavy disk swapping while parsing a PovRay scene. Of course this got me thinking and experiencing! And in order not to waste any of my precious thinking ;-) .... it finishes on the web, so you can enjoy it too.

This week end was Monte-Carlo grand prix in Monaco. It put me in the mood for some formula 1 modeling on Friday night. So I sat in front of my PC and using the 3D car preview of GP2edit (an unofficial windows utility to modify Microprose GP2 sim) to help me with proportions I quickly built a F1 model. Well, quickly might be a big word as it took me few hours to get it done. Anyway, I almost constantly had Mike's remarks in my head when modeling the car and tried my best to take advantage of the splines to use as little patches as possible. The result is a compact model that still manage to catch most of the curves of a real F1 racing car. Even if this model is not finished yet I thought I could use it to make some tests on patches and polygons with PovRay. To help me with my mission, I would use the new sPatch v1.0b3 export options, Keith Rule's Win converter to Pov and Winpov v3.01.

The experimental procedures!

I wanted to see by myself the differences between polygon based and spline based models. I already had some ideas of what they could be but I thought a real test, some rendered images and few statistics would help me have a better understanding of the issue. So I used my newly created sPatch Formula 1model to investigate. Using the enhanced functions of sPatch v1.0b3, I exported the model as:

		a POV scene (using bicubic patches only).
		a DXF file with 8 polygons/patch.
		a DXF file with 32 polygons/patch.
		a DXF file with 98 polygons/patch.

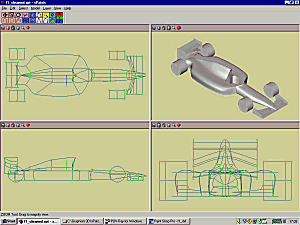
I used wcvt2pov v2.7 (a 3D converter by keith rule) to convert the DXF files into Pov 2.2 files. For all of them I used the triangle smoothing function to obtain the best possible render of the triangle meshes. I also created one file without smoothing using the DXF file with 8 polygons/patch. I loaded all these generated pov files into Winpov, added a checked plan and changed camera values and light setting to obtain similar shots of the models. After rendering each image, I read PovRay statistic window and noted significant values.

The raw results:

All images were rendered on a Pentium ® 133 with 512 Kb of cache memory and 32 Mb of main memory.
Resolution was 320x240 and no antialiasing was applied. Rendering was done with povray for Windows 3.01 under windows 95. Data collected from Winpov were parsing time, rendering time, total time and peak memory use during rendering. 

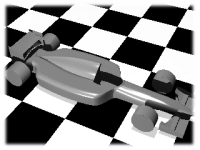
Bicubic Patches: parse time: 2 sec render time: 46 sec total time: 48 sec memory use: 253 Kb

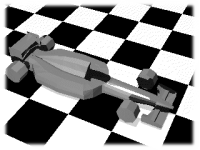
8 polygons/patch (no smoothing): parse time: 1 sec render time: 23 sec total time: 24 sec memory use: 631 Kb

8 polygons/patch: parse time: 1sec render time: 27sec total time: 28 sec memory use: 631 Kb

32 polygons/patch: parse time: 6 sec render time: 28 sec total time: 34 sec memory use: 2887 Kb

98 polygons/patch: parse time: 24 sec render time: 30 sec total time: 54 sec memory use: 8771 Kb

Looking at the images and the statistics above, few things appear:

	Bicubic patches are the most efficient method both for quality of the image and memory utilisation.
	polygon smoothing greatly improve quality of the image for polygon based models but extent render time by 5% to 10% (This would need more testing to get reliable estimation).
	Increasing polygon density increases quality but consumes memory VERY fast. It also greatly increases parsing time .... this make sense as parsing a mesh merely consists in putting the mesh in memory!
	polygons can achieve similar quality at the expense of memory use and to a smaller extent render time.
	Smoothing polygons allow the use of low resolution model without big loss of quality.
	Even a low resolution mesh uses twice as much memory as the patch based model.
	polygons models are prone to rendering artefacts (lost faces or normal problems). In this simple test, one face was lost on the 32poly/patch render and one normal problem appeared in the 98 poly/patch.
	my tip: If you are making render test on a complex scene use a low resolution polygon mesh with smoothing to gain render time with minimum quality loss.

Do you really need more? It looks quite clear to me. If you can, use patches rather than polygons for curvy objects. If speed is the bottom line and you have tons of RAM ... then use medium resolution polygon meshes with edge smoothing .... but you will always have problems in case of close looks. Patches don't have problems of resolution as they are mathematical definition of the curve. They also require less memory but a bit more time to render.

The final result is a victory of patches over polygons by a fairly large margin when speed isn't critical

>>> erratum <<<

While re-reading the PovRay documentation's paragraph about Bicubic Patches, I realised that what I was writing earlier might be badly interpreted. Patches ARE a mathematical description of a curvy surface but PovRay actually convert each patch into a triangle mesh during render. The difference in render quality comes from the fact that the meshing resolution applied by POV during render is adaptive which means more triangle are created where the curve is steep and less where flat.